Teaching about human probability judgments is like leading sheep to slaughter. “You know I’m setting you up for failure,” I tell my students. “And even though you know this, you’ll still fail.” I then toss out a few logical conundrums and listen to their confident—yet predictably wrong—responses.
A classic example is the Linda problem, first proposed by psychologists Amos Tversky and Daniel Kahneman in the 1980s. You should give it a try right now:
Linda is 31 years old, single, outspoken, and very bright. She majored in philosophy. As a student, she was deeply concerned with issues of discrimination and social justice, and she also participated in anti-nuclear demonstrations.
Which is more probable?
Linda is a bank teller.
Linda is a bank teller and is active in the feminist movement.
If you said that situation 2 is more probable than situation 1, congratulations! You’re a normal human being. You’re also wrong—at least, according to classical logic.
The Linda problem illustrates what’s known as the conjunction fallacy, which is the false belief that two events occurring together can be more likely than either of those events by itself. We can demonstrate that situation 1 is more likely than situation 2 by using a Venn diagram with two circles, one for “Bank Teller” and one for “Feminist.” The situation of being “Bank Teller and Feminist” lies in the intersection of these two circles.
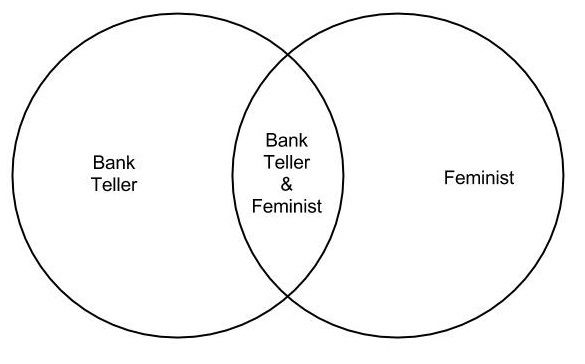
“Yes, but!” you’re protesting right now, as do my students at this point. And I agree: Situation 2 just feels like the right answer.
One issue with the Linda problem has to do with the way it’s worded. Most people interpret the first sentence to mean:
Linda is a bank teller and is not active in the feminist movement.
However, that’s not what the first sentence says. Instead, it means:
Linda is a bank teller and either is or is not active in the feminist movement.
No doubt this explanation only frustrates you even more. And it should, since it violates accepted norms of language use. Language isn’t always logical, though. That’s why the rules of classical logic were invented by Ancient Greek philosophers and developed by medieval scholars—to safeguard against the fallacious reasoning inherent in language.
Even when you clearly understand the meaning of situation 1, you probably still have a nagging feeling that situation 2 should be more likely. Famous paleontologist and science writer Stephen Jay Gould called the Linda problem a “cognition illusion,” much like the visual illusions we can’t help but see even though we know we’re being tricked.

Classical logic was a driving force in the scientific revolution because it provided a pretty good model for how the natural world around us works. However, the logic of Newtonian physics faced a double challenge in the early twentieth century. At the macro-level of stars and galaxies, Einstein showed that relativity was a better model than Newton’s laws. And at the micro-level of electrons and photons, physicists like Werner Heisenberg and Niels Bohr replaced Newtonian with quantum mechanics.
Quantum mechanics follows a different set of rules for calculating probabilities from those used in the middle level of the Newtonian universe that we experience. In other words, different levels of the universe follow different rules of logic. Since humans occupy the middle level, you’d think that human reasoning should be consistent with classical logic. And the fact that it isn’t has baffled psychologists for decades.
Recently, Ohio State University psychologists Jerome R. Busemeyer and Zheng Wang have made a “quantum leap” in understanding why we fall for the conjunction fallacy. Although their argument quickly becomes very technical, their main point is quite easy to follow. If you calculate the probabilities in the Linda problem according to the rules of classical logic, “Banker” is a more likely scenario than “Banker and Feminist.” However, if you calculate the probabilities according to the rules of quantum logic, “Banker and Feminist” is more likely than just “Banker,” in line with human intuition. This is because quantum logic takes prior conditions into account in a way that classical logic doesn’t.
The researchers maintain that a wide range of human cognitive processes are better described by quantum rather than classical logic. However, as they quickly point out, they are definitely not suggesting the brain is any sort of quantum computing device. They also strongly distance themselves from New Age pseudoscientific notions of quantum mind or quantum consciousness.
Quantum effects have no influence on human thought processes, but there are structural similarities between the quantum world and the social lives of humans. In particular, both exhibit a high degree of ambiguity and interrelatedness. Thus, quantum logic may be a better model for judging probabilities in human relationships.
Evolution has crafted human brains to be efficient processors of social information. So when it comes to making judgments about the likelihood of other people’s behavior, it’s not surprising to find it working more along the lines of quantum than classical logic. Perhaps, then, human intuitions aren’t nearly as illogical as psychologists have made them out to be.
References
Busemeyer, J. R. & Wang, Z. (2015). What is quantum cognition, and how is it applied to psychology? Current Directions in Psychological Science, 24, 163-169.
Gould, S. J. (1988, Aug. 18). The streak of streaks. The New York Review of Books.
Tversky, A. & Kahneman, D. (1983). Extensional versus intuitive reasoning: the conjunction fallacy in probability judgment. Psychological Review, 90, 293-315.
David Ludden is the author of The Psychology of Language: An Integrated Approach (SAGE Publications).




