Verified by 
Key points
- Report card grades should measure students' overall performance and knowledge.
- When calculating a grade by averaging performance, more extreme values are weighted more heavily than those close to the mean.
- Because grades typically run from A to F (100 to 50), giving students a zero for a missed assignment significantly affects their grade.
- Assigning a 50 instead of a zero penalizes missed assignments but balances the possibility of bringing a grade up.
Report card grades are supposed to measure how well students have performed in class.
- Performance is a construct: What we are trying to measure.
- Report card grades are measures: They mean to capture the construct.
If grades are valid, people with high grades will perform better than those with lower grades. Although we hope that grades also reflect learning–people who learned more have higher grades–we know that's not always true. Being sick, having a chaotic home that makes it hard to do homework or study, or reading ability can all affect grades differently than they affect learning.
Measures of Central Tendency
Report card grades typically reflect central tendencies. Measures of central tendency are intended to be a single number (or grade) that captures the full construct (performance). A report grade usually captures several different assignments, which often vary.
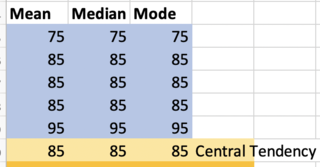
Psychologists use three indicators of central tendencies–the mean, the median, and the mode. Each minimizes a different type of error.
- The mode is the most common value. In the figure below, students have five grades: a 75, three 85's, and a 95. If you had to guess what grade someone got on an assignment and said "85," you'd be wrong fewer times (have less error) with that guess than by guessing anything else.
- The median is the value that is in the middle of the distribution. If you use "85" to reflect how well a student did, you are wrong by 10 points for their 75, by 0 points for all three 85's, and you're wrong by 10 points for that 95 they got. In other words, your summed error is 20. The median minimizes summed error.
- The mean or average is when we take all the numbers in a distribution, add them together, and divide by how many numbers there are. Have you ever considered why that is a good measure of central tendency? What the average does is minimize summed squared error. So your "error" for a mean of 85 and a grade of 75 is 10. For 85, it is zero, and for 95, it is 10. The squared error is thus 102 + 02 + 02+ 02 + 102: 200. No number will give you a smaller summed square error than the mean.
Because you are squaring errors to determine the mean, it is sensitive to outliers (sensitive to values far from the center). That's why many of us were taught always to use means unless a distribution was very lopsided.
When a distribution is lopsided, you have large errors. When you have large errors in lopsided distributions, most of us were taught that's when you use medians. In other words, means are the standard because they are the 'fairest'. Medians were invented to fix this unusual problem means have. That's not actually the case. Medians minimize error. Means minimize BIG errors. We are weighting large errors by squaring them and moving the mean until we find the number that does that best.
I understand means, medians, and modes. What’s that got to do with giving zeros for missing assignments?
In the figure above, if you calculate a report card grade using the mean, median, or mode all, you will get the same grade–an 85 or B.
Let's look at what happens if a student misses an assignment, and the teacher uses an average to compute their grade.
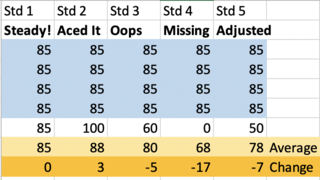
In this example, the students got 85s on the first four assignments. What happens on Assignment 5?
- Student 1 got an 85 on Assignment 5 and earned their expected 85.
- Student 2 aced it! They got a 100, raising their grade from an 85 to an 88 (a three-point gain).
- Student 3 did poorly on Assignment 5, earning a 60. This dropped their report grade by five points to an 80.
All of these changes are more or less what we expect.
But now look at Student 4, who missed the last assignment. They were assigned a zero. This dropped them a full 17 points (from 85 to 68).
Notice that doing as well as possible–getting a 100 like Student 2–can only raise your grade by three points. However, doing as poorly as possible– skipping the assignment–drops your grade by 17 points.
Why? Because averages are very sensitive to outliers. One hundred is only 15 points higher than the average of the first four grades. It is relatively close to the central tendency. On the other hand, a zero is a full 85 points lower. It has a very large error, and the average has to move a lot to minimize the sum squared error.
That's because the functional range of grades is not zero to 100. No teacher I've ever seen has a class with an average of 50 and a range from zero to 100. Instead, most teachers hope for an average of perhaps 85. In reality, grades go from F (a 50) to A+ (100). That's the functional range for grades.
What if we assigned the lowest grade in the functional range for missing assignments instead of a zero?
As I wrote in the beginning, grades are meant to assess performance. What would happen if we assigned a solid F for missing grades? In other words, what if we assigned 50s for missing grades instead of zeros? Look at the last column, with Student 5. When assigned a 50, Student 5's grade drops seven points after the last assignment–from an 85 to a 78. That's a significant penalty but not insurmountable.
Is assigning students 50s for missing grades instead of zeros fair? Let's look at the students. The student who got four Bs and a D (Student 3) would earn an 80 on their report card (B-). The student who got four Bs and missed the last assignment and got a 50 for it (Student 5) would earn a 78 (C+). Had that student's teacher followed the more standard practice of assigning a zero for the missing assignment, they would have earned a 68 (D+).
Deciding how to calculate grades needs to reflect the teacher's belief about which grade best reflects the student's performance. It needs to be consistent across students–unbiased. But given the functional range of grades 50 to 100, there is an argument to be made that counting missing assignments as 50s produces fairer grades than assigning them zeros.
