Verified by 
In past posts, I’ve discussed how subjects in the lab play a variety of theoretical decision games of cooperation and conflict, from the Prisoners’ Dilemma game that’s most widely known to a broad public, to the Public Goods Game (or Voluntary Contribution Mechanism) that’s been studied for decades by experimentalists around the world, and the Trust Game about which more than one post has appeared here.
The Centipede Game was invented by a political economist to test the intuition that people would rarely pass up the opportunity to make money by cooperating for at least a little while with their partner in play, even if the hyper-rationality of game theory implies there’ll be zero cooperation. The tendency Robert Rosenthal was expecting to document is largely the same as I’ve reported being observed frequently in the Prisoner’s Dilemma, the Public Goods Game, and the Trust Game, in which players can also make more money on average if they violate the requirement of strictly rational selfishness, as long as an adequate number of others do the same. The Centipede Game, however, is the “mother of all norm busters” when it comes to illustrating the human penchant for cooperation, and you’ll see why as soon as I’ve described for you the game displayed in the accompanying image.
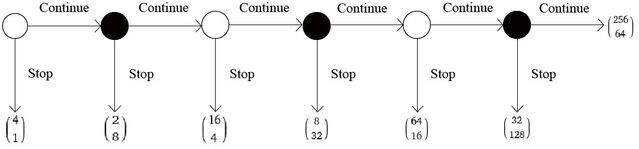
Suppose that two players, call them White and Black, are invited to enter into an interaction in which they can take turns deciding between a “Stop” move that ends the game with the payoffs to which the downward arrow points, and a “Continue” move that lets their counterpart decide whether to Stop or Continue. Each white circle represents a decision node at which player White chooses Stop or Continue, each black circle is a node at which player Black chooses between the same two options. The interaction goes on until one of the players chooses Stop or until the last move is reached and the player concerned—Black—chooses Continue. The top and bottom numbers in parentheses indicate the amounts earned by White and Black, respectively. They have the special property that the longer the game goes on for, the larger is the pot of money being divided between White and Black, but with each succeeding decision node, the decider risks losing money if her counterpart chooses an immediate Stop. For essentially the same reason that traditional game theory which assumed players to be selfish and rational predicts no trusting in the Trust Game and no cooperating in the Prisoners’ Dilemma and the Public Goods Game, that body of theory predicts unambiguously that no Continue decision will ever be made in the Centipede Game. As is usual with multi-round games, the logic is that of “backward induction.” Let’s review that logic again now.
Suppose that the right-most black decision node were reached, so Black would get to choose between (1) the Continue move, which gives White 256 and Black 64, and (2) the Stop move, which gives White 32 and Black 128. From the standpoint of the mini-society consisting of the two players, the first choice is clearly better, because it entails that there are 320 (= 256 + 64) money units (maybe dollars) to divide between the two, while the second option means there’s only half as many units, or 160 (= 32 + 128) available. But the kicker is that the two players are prevented by the setting from entering into any form of agreement. Were contracts an option, then both players could achieve more earnings than at the (32, 128) outcome, since Black could select Continue at the final node, thereby earning 64 while causing White to earn 256—a total of 320. That’s sixty-four times as much money as would be earned if White followed the “selfishly rational” prediction of game theory! Under such a contract, White could then fulfill a promise to give 96 of her earnings to Black, and both would end up with 160—forty times White’s earnings in the “selfishly rational” prediction—the prediction that White chooses STOP at node 1—and a hundred and sixty times higher earnings for Black! The trouble is that with no communication possible, and no contract enforcement available to be employed even if communication could happen, a selfishly rational White would hold on to all 256 and leave Black with only 64, were Black to choose Continue at the rightmost Black node, so the (32, 128) outcome Black gets by choosing Stop is Black’s best option there. The same logic applies at each and every node. At the starting node where White has to choose between ending the game with 4 or handing off to Black through continuation, White faces the risk that Black will opt for an ending, which would give White only 2. Since Black will be tempted to end with the 8 that is available to Black at the first Black node (node 2) rather than risk ending up with only 4 if White opts out at node 3, Black would be selfishly rational to opt out at node 2, and therefore White should forego continuation at node 1 so as to lock in White’s payoff of 4, however measly it is in comparison to payoffs available farther rightwards on the decision chain. Traditional game theory and economics thus predicted that White would choose Stop at the first (leftmost) node every time!
If people were asked to play the game for real money (with the numbers along the line being dollar amounts), if all were as selfish and rational as traditional economics and game theory suppose, and if one of every two players were randomly assigned the White and the other the Black role, then we would expect average earnings in the version of the game that the diagram illustrates to be $2.50 (half earn $4, half earn $1). That’s our prediction if we are traditional game theorists like John Nash. In practice, though, it’s rare for subjects to stop at the first node, and earnings of $20 or $30 on average have been the norm in dozens of experiments.
I like to use this game to provide intuition as to why evolutionary forces may have made the human being a cooperative creature rather than the hyper-rational selfish creature of the old game theory models. Real humans cooperate. In the environment in which we evolved as mobile foragers, we cooperated on matters of child rearing, of defense of the band against dangerous animals, of hunting, of preventing the embers of the campfire from being extinguished. Figuratively speaking, we may have on average needed the calories associated with outcomes such as the 8, 32 of node four or the 64, 16 of node five. Whenever the evolution of our psyches tilted some genetic dynasty of our ancestors toward greater selfishness, that group would have gradually died out due to insufficient average payoffs. Only those groups that struck a viable balance between rational individualism and solidaristic cooperation would have regularly obtained enough calories and protection from the elements to have made it through the thousands of generations that got us to the present day. We are the descendants of cooperators, and only a handful of hyper-rational individualists in laboratory trials of Rosenthal’s centipede game are actually observed to Stop at the first node, because that’s not who we are. Whatever potential ancestors of ours were also inclined to stop always at the leftmost node were the potential ancestors of Homo economicus, the hyper-rational hyper-selfish creature of traditional economic theory. But that hypothetical creature never managed to evolve, because an average payoff of two-and-a-half always led to starvation and a lack of surviving descendants.
Experimentation with variants of the game that explicitly place more versus less weight on group average outcomes in order to study the evolutionary dynamics of this cooperation problem in a careful manner will hopefully be reported in this space in a future post. By adding a bit of weight to the group average payoff, it should be possible to mimic in the lab a group selection model resembling the one discussed by authors like Rob Boyd, Joe Henrich, Herb Gintis, and Sam Bowles. Stay tuned.
